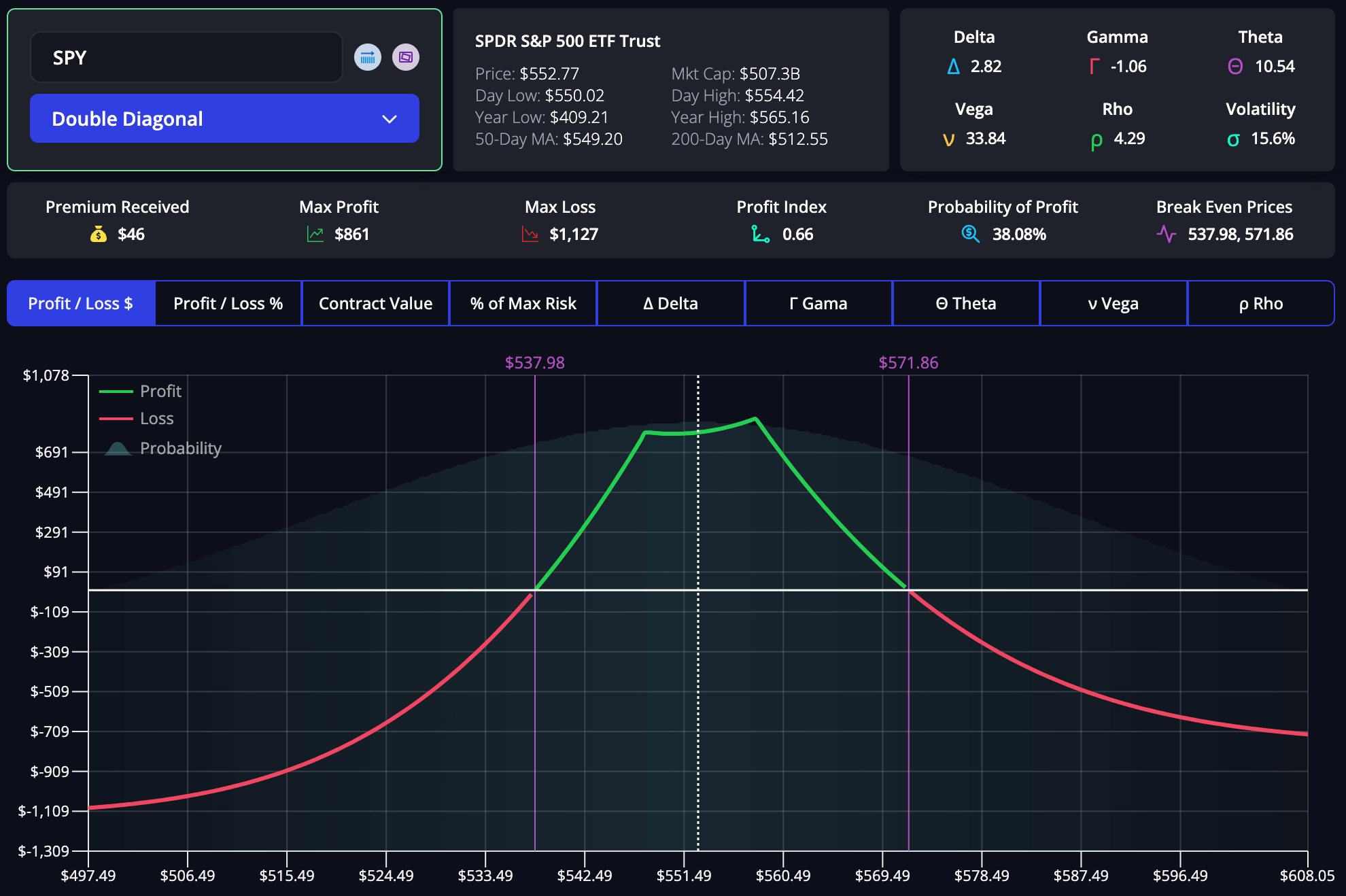
Complete Guide to Options Trading with Greeks

Key Takeaways

• Master the Greeks: Understand Delta, Theta, Gamma, Vega, and Rho.
• Informed Decisions: Use the Greeks to assess risk and potential rewards.
• Optimize Strategies: Leverage the Greeks to refine your trading approach.
• Real-World Examples: See how the Greeks impact pricing in different scenarios.
• Advanced Techniques: Implement Delta-neutral strategies, Gamma scalping, and more.
• Trading Tools: Analyze the Greeks with an options profit calculator.

Why It Matters

• Maximize Profits: Understanding the Greeks helps you make smarter trades and optimize profits.
• Risk Management: The Greeks provide insights into risk, allowing for better hedging and portfolio management.
• Strategic Advantage: Leveraging the Greeks gives you a strategic edge in the complex options market.
• Enhanced Decision-Making: Knowledge of the Greeks leads to more informed and confident trading decisions.
• Financial Success: Mastery of the Greeks is crucial for achieving long-term success and stability in options trading.

Imagine having the power to predict and control your trading outcomes with precision.

Options trading provides this power, enabling you to hedge risks, speculate on price movements, and leverage positions for maximum profit. At its core, options trading involves contracts that give you the right, but not the obligation, to buy or sell an underlying asset at a predetermined price before a specified expiration date. This flexibility and leverage come with complexities, and the key to navigating them successfully lies in understanding the Greeks—Delta, Theta, Gamma, Vega, and Rho.

The Greeks are your essential tools for assessing the risks and potential rewards of your options positions. These metrics measure the sensitivity of an option's price to various influencing factors, such as changes in the underlying asset’s price, time decay, volatility, and interest rates.

By mastering the Greeks, you can make more informed decisions, optimize your strategies, and significantly enhance your profitability in the options market. Dive in, and discover how understanding the Greeks can transform your trading prowess and lead you to greater financial success.

Delta (Δ)

Delta measures the rate of change of the option's price relative to a one-point move in the underlying asset's price.

• Call Options: Delta ranges from 0 to 1. A Delta of 0.5 means the option’s price will theoretically move $0.50 for every $1 move in the underlying asset.
• Put Options: Delta ranges from -1 to 0. A Delta of -0.5 means the option’s price will theoretically move -$0.50 for every $1 move in the underlying asset.
• Directional Risk: Delta indicates the directional exposure of the options position. Higher Delta implies higher sensitivity to price movements in the underlying asset.

Delta Market Scenarios

Consider a scenario where a trader holds a call option on a stock currently trading at $50. If the Delta of the call option is 0.6, a $1 increase in the stock price to $51 would result in an estimated $0.60 increase in the call option’s price. Conversely, if the trader holds a put option on the same stock with a Delta of -0.4, the $1 increase in the stock price would decrease the put option's price by approximately $0.40.

In volatile market conditions, these Delta values can significantly impact trading decisions. For instance, if a tech stock is experiencing rapid price increases due to a favorable earnings report, call options with high Delta values will see substantial price appreciation, offering significant profit opportunities for the trader.

Delta Neutral Strategies

Delta-neutral strategies are designed to hedge portfolios and reduce directional risk by ensuring that the total Delta of the portfolio is zero. This means that the positive and negative Deltas balance out, resulting in minimal sensitivity to the underlying asset's price movements. Traders achieve this by combining options and the underlying asset in such a way that the net Delta of the positions cancels out.

For example, if a trader owns a stock with a Delta of 1.0 (since each stock’s Delta is always 1), they can create a Delta-neutral position by buying a put option with a Delta of -0.5 and a call option with a Delta of -0.5 on the same stock. The net Delta of this portfolio would be 0 (1 - 0.5 - 0.5), effectively neutralizing the directional risk.

Delta Hedging

Delta hedging is a strategy used to maintain a balanced portfolio by continuously adjusting the positions to keep the Delta at a desired level. This approach involves buying or selling the underlying asset or options to offset the changes in Delta, ensuring that the portfolio remains hedged against price movements.

For instance, suppose a trader holds a call option with a Delta of 0.6 on a stock. If the stock price rises, increasing the Delta to 0.7, the trader can sell a portion of the underlying stock to reduce the Delta back to 0.6. Conversely, if the stock price falls, decreasing the Delta to 0.5, the trader can buy additional shares to bring the Delta back up.

Delta hedging requires continuous monitoring and adjustments, especially in volatile markets where the Delta can change rapidly. This dynamic adjustment helps traders manage risk and maintain a balanced portfolio, ensuring that they are not overly exposed to adverse price movements in the underlying asset.

Theta (Θ)

Theta measures the rate of decline in the value of the option due to the passage of time, also known as time decay.

• Time Decay: Theta is generally negative for both calls and puts, indicating that options lose value as expiration approaches.
• Short-Term vs. Long-Term: Theta decay accelerates as expiration nears, especially for at-the-money options.
• Strategic Decisions: Traders may use Theta to gauge the best time to enter or exit a position, aiming to minimize time decay losses.

Short-Term Options Theta Example

Consider a trader who buys a call option on a stock with an expiration date one month away. Initially, the option has a Theta of -0.05, meaning it loses $0.05 in value each day due to time decay.

As the option nears expiration, the Theta increases to -0.10, causing the option to lose $0.10 per day. This accelerated decay significantly impacts the trader's potential profit if the stock does not move favorably quickly.

Long-Term Options Theta Example

In contrast, a trader buys a long-term call option (LEAPS) with an expiration date one year away. The initial Theta is -0.01, reflecting a slower time decay rate. Even as months pass, the Theta remains relatively low, allowing the trader to hold the position longer without significant loss from time decay. This highlights the advantage of longer-term options for traders looking to minimize the impact of Theta.

Theta in Covered Calls

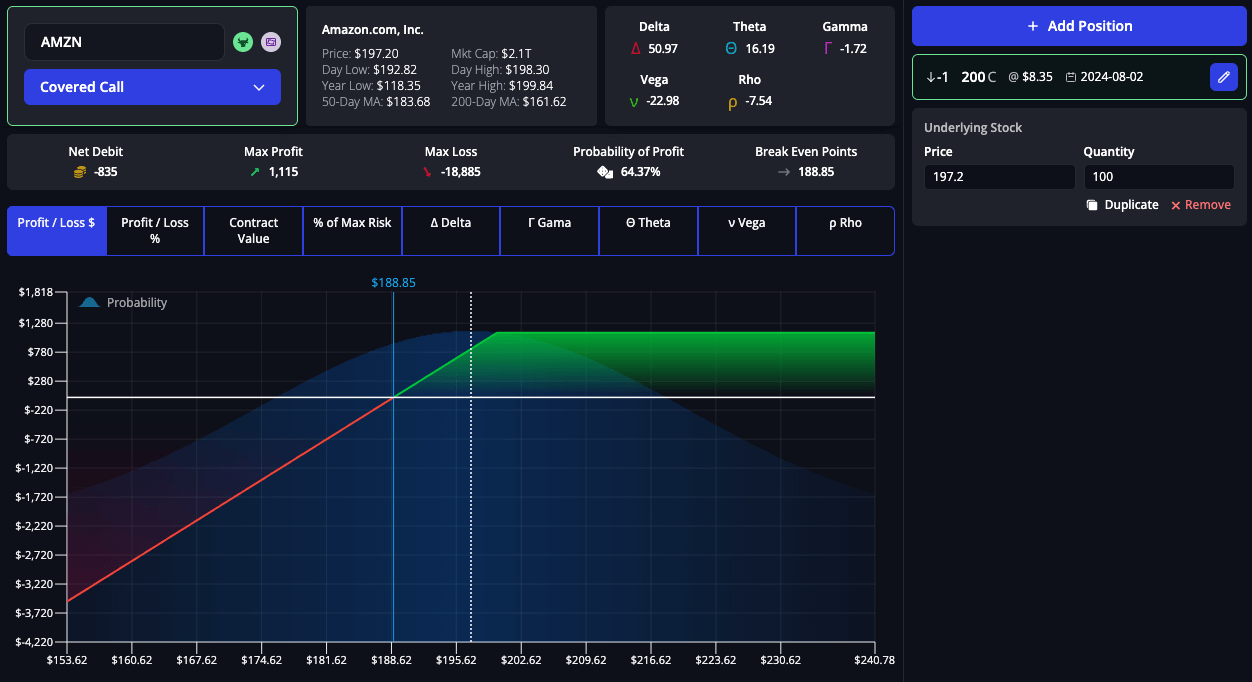
Theta is a crucial consideration in covered call strategies, where a trader holds a long position in a stock and sells call options on the same stock. The goal is to generate income from the premiums received for the call options.

Since Theta is negative, the options sold will lose value over time, benefiting the seller. This strategy works well in stable or mildly bullish markets, where the stock price does not exceed the strike price of the sold call options.

Theta in Cash-Secured Puts

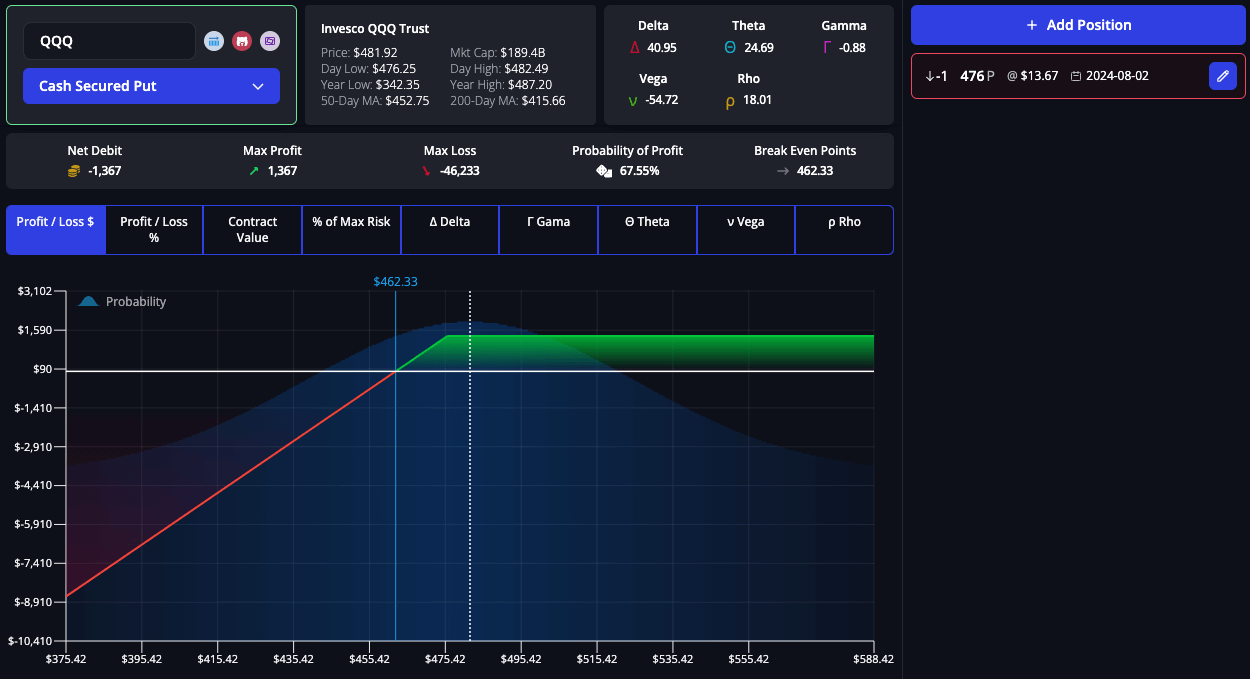
In a cash-secured put strategy, a trader sells put options without holding a corresponding position in the underlying asset. The trader collects the premium from selling the put option, hoping that the option will expire worthless due to time decay (Theta).

As expiration approaches and Theta accelerates, the option loses value, which can be profitable for the trader if the underlying stock remains above the strike price.

Managing Theta by Rolling Options Positions

Rolling options involves closing an existing options position and opening a new one with a later expiration date. This technique can manage Theta decay by extending the time horizon.

For instance, a trader with a call option nearing expiration and experiencing high Theta decay might roll the position to a later expiration, reducing the immediate impact of time decay and providing more time for the underlying asset to move favorably.

Profiting from Theta with Time Spreads (Horizontal Spreads)

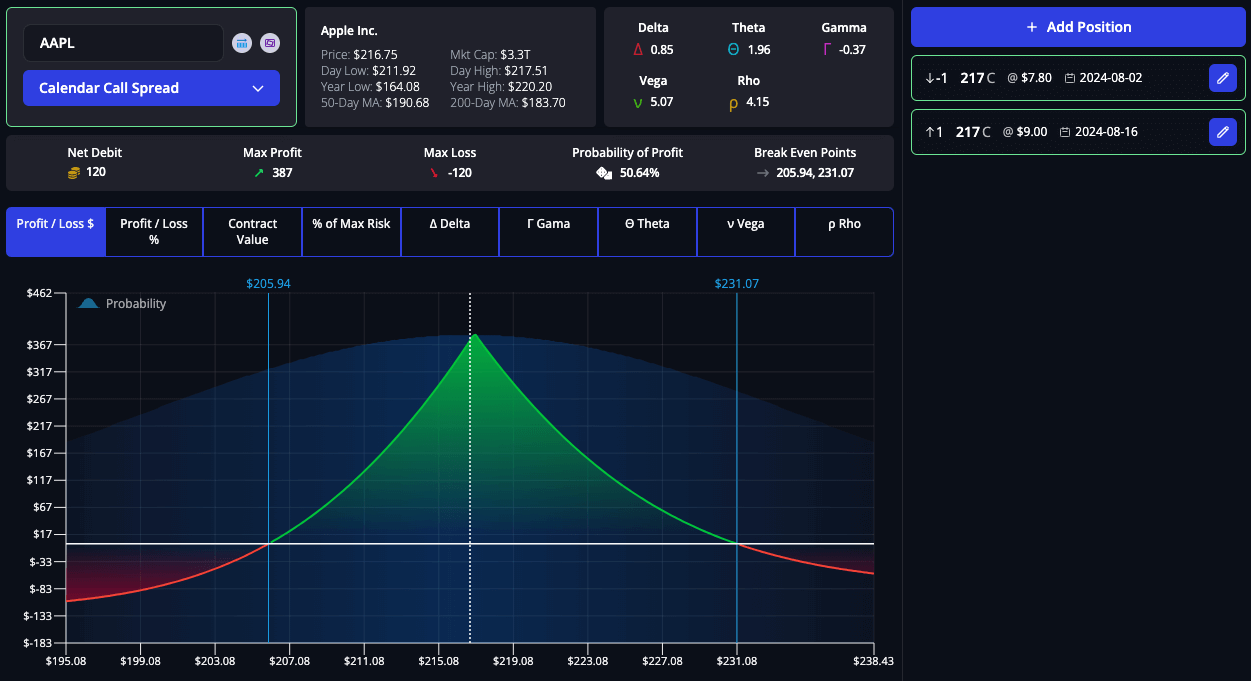
Time spreads, also known as horizontal spreads or calendar spreads, involve buying and selling options with the same strike price but different expiration dates. This difference in time decay rates can be advantageous, as the trader benefits from the rapid decay of the short-term option while maintaining the value of the long-term option.

For example, a trader might sell a near-term option with high Theta and buy a longer-term option with lower Theta. The goal is to profit from the accelerated time decay of the short-term option while holding a position that retains more value over time.

Gamma (Γ)

Gamma measures the rate of change in Delta relative to a one-point move in the underlying asset’s price.

• Delta Sensitivity: High Gamma indicates that Delta can change rapidly, leading to larger price swings in the option for small moves in the underlying asset.
• Risk Management: Traders often monitor Gamma to manage the stability of Delta, especially near expiration or around significant price levels.
• Hedging: High Gamma positions require more active management to maintain a desired Delta exposure.

Earnings Announcements

Consider a trader holding options on a company’s stock just before an earnings announcement. The stock price is expected to move significantly based on the results. In this high-volatility period, the Gamma of at-the-money options can be quite high.

If the stock price jumps dramatically post-announcement, the Delta of these options will change rapidly, leading to significant changes in the option's price. Traders need to monitor Gamma closely to adjust their positions accordingly, potentially making quick profits or hedging against adverse movements.

Market Crashes

During market crashes, volatility spikes, causing Gamma to increase for many options. For example, during the 2008 financial crisis or the COVID-19 market crash in March 2020, options traders experienced extreme Gamma, leading to rapid changes in Delta. Traders with high Gamma positions had to quickly adjust their portfolios to manage the increased risk and avoid substantial losses due to the sharp market movements.

Gamma Scalping

Gamma scalping is a strategy that involves continuously buying and selling the underlying asset to profit from small price movements while maintaining a Delta-neutral position. The goal is to capitalize on the volatility and the rapid changes in Delta indicated by high Gamma.

A trader starts with a Delta-neutral position by holding options and an offsetting amount of the underlying asset. As the underlying asset's price moves, the Delta changes due to Gamma. The trader buys or sells the underlying asset to bring the Delta back to neutral.

For example, if the price of the underlying asset rises, the Delta of a call option increases, making the overall position Delta-positive. The trader would then sell the underlying asset to bring the Delta back to zero.

This process of continuously adjusting the Delta allows the trader to capture profits from the small price movements of the underlying asset, leveraging the high Gamma of the options position. Gamma scalping can be particularly profitable in volatile markets where price swings are frequent.

Risks Associated with High Gamma Positions

High Gamma positions come with significant risks, primarily due to the rapid changes in Delta. Traders need to be vigilant and prepared to make frequent adjustments to their portfolios. The main risks include:

• Rapid Delta Changes: High Gamma means that even small moves in the underlying asset can lead to substantial changes in Delta, requiring constant monitoring and adjustments.
• Increased Transaction Costs: Frequent buying and selling of the underlying asset to maintain a Delta-neutral position can lead to high transaction costs, eating into profits.
• Market Impact: In volatile markets, the speed at which Delta changes can outpace the trader’s ability to adjust positions, leading to unexpected losses.

Mitigating Gamma Risk

To mitigate the risks associated with high Gamma positions, traders can:

• Limit Position Sizes: Keeping positions smaller can reduce the overall risk and make adjustments more manageable.
• Use Stop-Loss Orders: Implementing stop-loss orders can help limit losses if the market moves against the position too quickly.
• Diversify Holdings: Diversifying across different underlying assets and options can spread the risk and reduce the impact of Gamma on the overall portfolio.
• Regular Monitoring: Continuous and vigilant monitoring of positions is essential, especially during periods of high volatility. Automated trading systems can help manage rapid adjustments more efficiently.

Vega (ν)

Vega measures the sensitivity of the option’s price to changes in the volatility of the underlying asset.

• Volatility Exposure: A higher Vega means the option’s price is more sensitive to changes in implied volatility.
• Volatility Trading: Traders may exploit Vega by trading options in volatile markets or using strategies like straddles and strangles.
• Risk Assessment: Understanding Vega helps in assessing how much the option’s price might move with changes in market volatility.

Impact of Implied Volatility on Different Options

Implied volatility (IV) represents the market’s forecast of a likely movement in the underlying asset’s price. It directly affects the premium of options:

• Call and Put Options: Both types of options increase in value with higher implied volatility. This is because higher volatility suggests a greater probability of the option finishing in-the-money.
• Out-of-the-Money (OTM) Options: These options are particularly sensitive to changes in implied volatility. A small increase in IV can lead to a significant increase in the price of OTM options.
• At-the-Money (ATM) Options: ATM options typically have the highest Vega, meaning their prices are most affected by changes in IV.

For example, during earnings season, a company’s stock might experience heightened implied volatility due to anticipated earnings announcements. Options traders need to monitor Vega to adjust their positions accordingly, capturing opportunities or hedging against risks associated with volatility swings.

Vega in Straddles

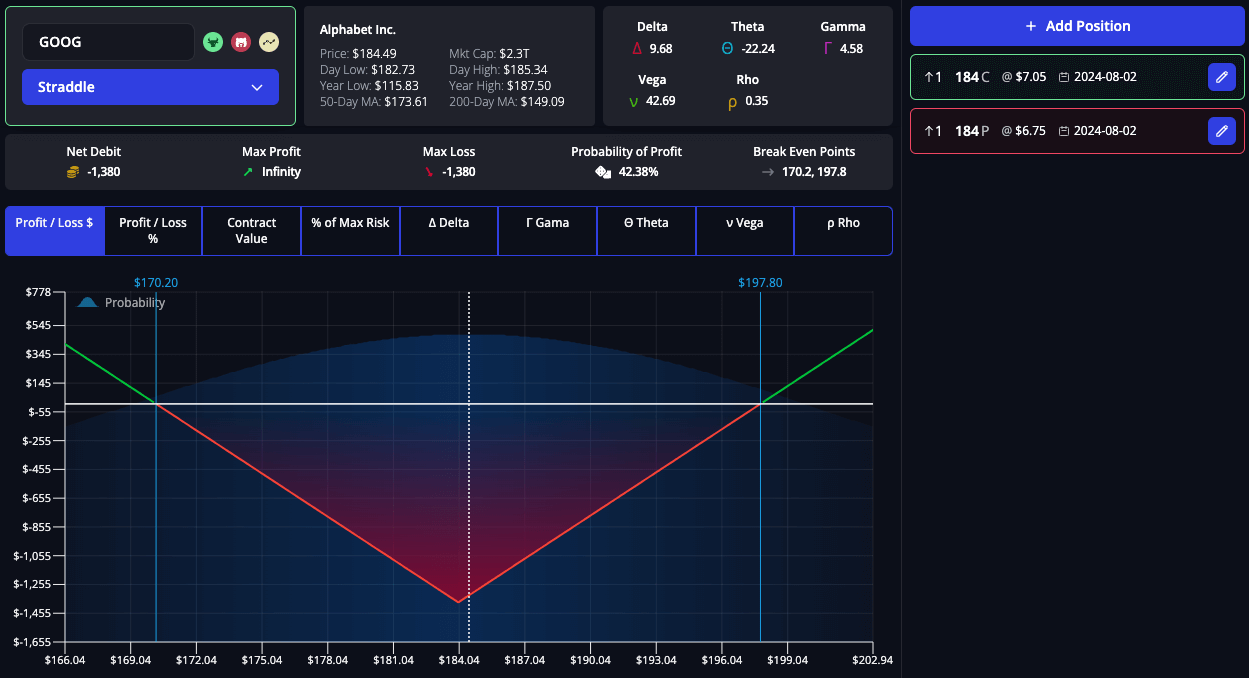
A straddle involves buying a call and a put option at the same strike price and expiration date. This strategy benefits from significant movements in the underlying asset’s price, regardless of direction.

• Role of Vega: High Vega indicates that the options will gain in value as implied volatility increases. Traders implement straddles when they expect a major price move or an increase in IV due to events like earnings announcements or economic reports.

Vega in Strangles

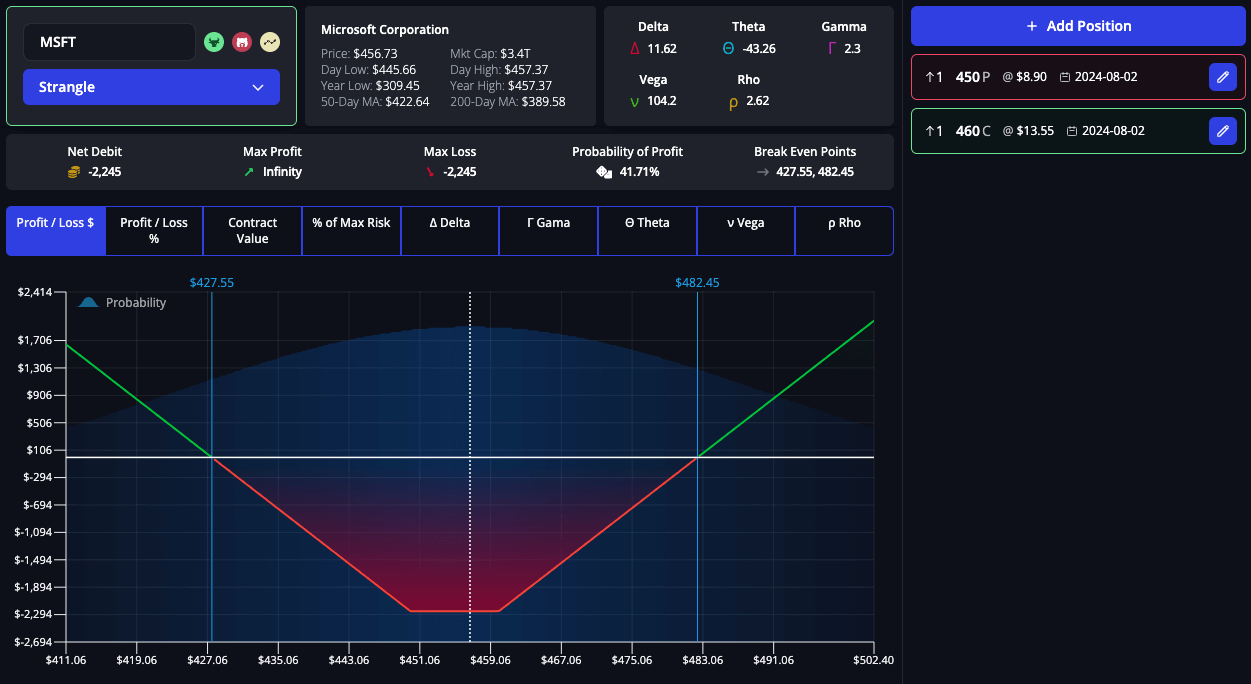
A strangle involves buying a call and a put option with different strike prices but the same expiration date. This strategy is similar to a straddle but provides a cheaper entry cost with a wider range of profitability.

• Role of Vega: Similar to straddles, strangles benefit from increases in implied volatility. Traders use strangles when they anticipate significant price movements but are unsure of the direction.

Vega in Iron Condors

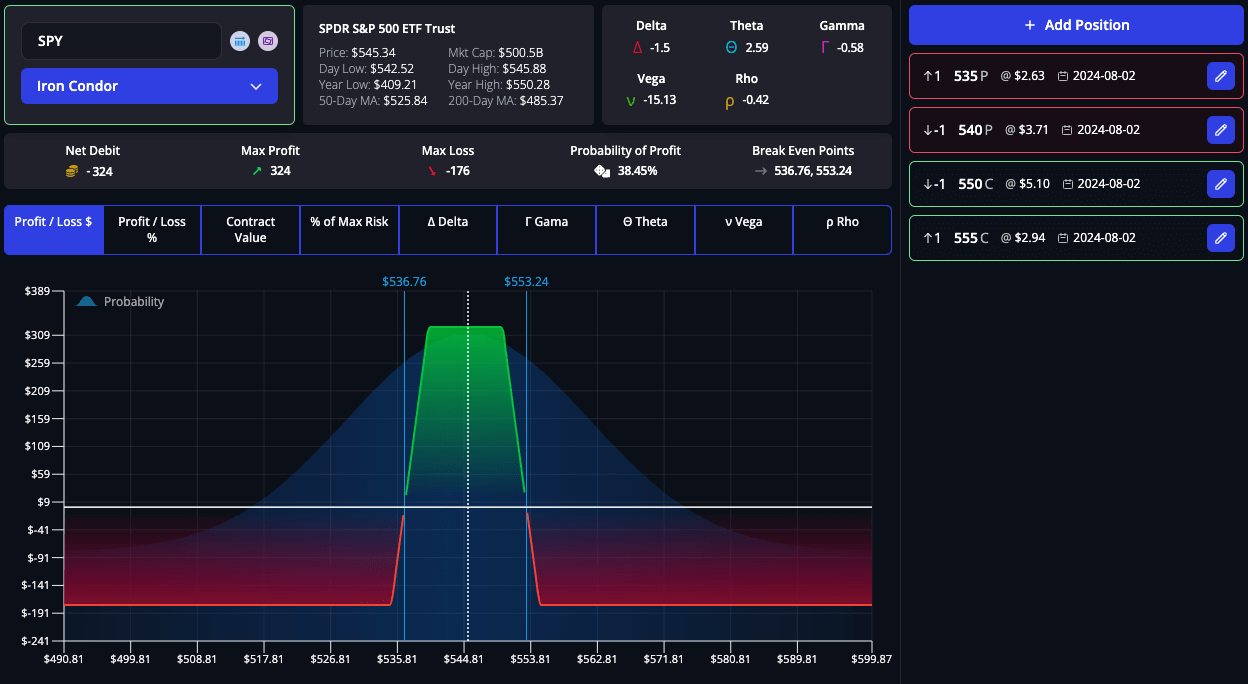
An iron condor involves selling an OTM call and put while simultaneously buying a further OTM call and put. This strategy profits from low volatility and a stable underlying asset price.

• Role of Vega: Vega negatively impacts iron condors. If implied volatility increases, the spread widens, leading to potential losses. Traders use iron condors when they expect low volatility and minimal price movement.

Historical Volatility

Historical volatility (HV) measures the actual price movements of the underlying asset over a specified period. It is a backward-looking measure based on past price data.

• Impact on Vega: While HV provides insights into the past volatility of an asset, it does not directly impact Vega. However, understanding HV can help traders make informed predictions about future volatility and its potential impact on option prices.

Implied Volatility

Implied volatility (IV) is a forward-looking measure, reflecting the market’s expectations of future volatility. It is derived from the current prices of options.

• Impact on Vega: Vega is directly influenced by changes in implied volatility. When IV increases, options with high Vega gain in value, and when IV decreases, these options lose value. Traders monitor IV to anticipate changes in option prices and adjust their strategies accordingly.

Comparing Historical and Implied Volatility

• Predictive Power: While HV offers a historical perspective, IV provides a market consensus on expected future volatility. Traders often use both to gauge volatility trends and inform their trading decisions.
• Strategy Development: Understanding the differences between HV and IV allows traders to develop strategies that capitalize on expected volatility changes. For instance, if IV is significantly higher than HV, it might indicate that options are overpriced, presenting opportunities for selling strategies like iron condors.

Rho (ρ)

Rho measures the sensitivity of the option’s price to changes in interest rates.

• Interest Rate Sensitivity: Call options typically have positive Rho, while put options have negative Rho. This means call options increase in value with rising interest rates, and put options decrease in value.
• Macro Factors: Rho is more significant for long-term options as short-term interest rate changes have less impact.
• Economic Considerations: Rho helps traders assess the impact of interest rate changes due to economic policy decisions on their options positions.

Historical Interest Rate Trends

Analyzing historical interest rate trends provides valuable insights into how interest rate changes have impacted options pricing over time. For example:

• Early 1980s: During this period, the Federal Reserve raised interest rates significantly to combat high inflation. As a result, the Rho of call options increased, leading to higher premiums, while the Rho of put options decreased, making them cheaper.
• 2008 Financial Crisis: The Federal Reserve cut interest rates to near zero to stimulate the economy. This drastic reduction decreased the Rho for call options and increased the Rho for put options, impacting options strategies that relied on interest rate movements.

Rho’s Impact on Long-Term Options

Long-Term Equity Anticipation Securities (LEAPS) are options with expiration dates longer than one year. Due to their extended duration, LEAPS are more sensitive to interest rate changes, making Rho a crucial factor in their pricing.

• Positive Rho for LEAPS Calls: A rising interest rate environment can significantly increase the value of LEAPS call options. For instance, if a trader holds a LEAPS call with a Rho of 0.25, a 1% increase in interest rates would theoretically increase the option’s price by $0.25 per share.
• Negative Rho for LEAPS Puts: Conversely, the value of LEAPS put options decreases with rising interest rates. A LEAPS put with a Rho of -0.30 would see its price drop by $0.30 per share for a 1% rise in interest rates.

Influence of Central Bank Decisions on Rho

Central banks, like the Federal Reserve, play a pivotal role in setting interest rates. Their decisions are influenced by economic indicators such as inflation, employment rates, and GDP growth. Major economic policies and central bank decisions can have profound impacts on Rho and, consequently, options prices.

• Quantitative Easing (QE): During periods of QE, central banks inject liquidity into the economy, typically lowering interest rates. This environment decreases Rho for call options and increases it for put options. Traders need to account for these changes when formulating their strategies.
• Interest Rate Hikes: When central banks increase interest rates to curb inflation, call options with positive Rho gain value, while put options with negative Rho lose value. For example, a 0.5% rate hike can lead to noticeable price adjustments in long-term options, making it essential for traders to anticipate these moves.

Rho Case Study: Federal Reserve's Policy Shifts

Consider the Federal Reserve's shift in monetary policy from 2020 to 2022. Initially, rates were kept near zero to support the economy during the COVID-19 pandemic. As the economy recovered, the Fed signaled a series of rate hikes to combat rising inflation.

• Impact on Options Prices: Options traders had to adjust their positions based on these signals. LEAPS calls became more attractive due to their positive Rho, while LEAPS puts required careful management to mitigate losses from their negative Rho.
• Strategic Adjustments: Traders anticipating rate hikes could buy call options or sell put options to capitalize on the expected increase in call premiums and decrease in put premiums. Conversely, traders expecting rate cuts might favor strategies that benefit from declining interest rates.

Mastering the Greeks: Your Path to Options Trading Success

Understanding and mastering the Greeks—Delta, Theta, Gamma, Vega, and Rho—is crucial for any options trader aiming to achieve long-term success. These metrics provide invaluable insights into the factors influencing options pricing, enabling traders to make informed decisions, manage risks, and optimize their strategies.

By incorporating the Greeks into your trading toolkit, you can enhance your ability to navigate the complexities of the options market and seize profitable opportunities.

Unlock Your Trading Potential with InsiderFinance

To further elevate your trading experience and maximize the benefits of understanding the Greeks, consider leveraging the powerful tools and resources offered by InsiderFinance.

Use the InsiderFinance options profit calculator to model the potential outcomes of your trades with high accuracy. This tool allows you to:

• Visualize Profit and Loss: See potential profit and loss scenarios for various strategies, helping you understand the impact of Delta, Gamma, and Theta on your positions.
• Evaluate Volatility Impact: Assess how changes in implied volatility (Vega) affect your trades, ensuring you are prepared for different market conditions.
• Analyze Interest Rate Changes: Factor in potential interest rate changes (Rho) and their impact on long-term options like LEAPS.
• User-Friendly Experience: Enjoy a seamless and intuitive user experience designed to simplify complex calculations, making it easier to make informed trading decisions.

Mastering the Greeks is your gateway to becoming a successful options trader. By understanding how Delta, Theta, Gamma, Vega, and Rho influence options pricing, you can make smarter, more strategic decisions.

Leverage the advanced tools and insights from InsiderFinance, including their exceptional options profit calculator, to enhance your trading strategies and achieve the success you aspire to.

Start your journey to options trading mastery today—try the InsiderFinance options profit calculator and transform your trading experience.